Hola hoy les voy a dejar unos ejercicios sobre arboles binarios implementados en prolog.
Un poco de teoría:
En Ciencias de la Computación, hablamos de un árbol como una estructura, que contiene un nodo padre y dos nodos hijos, un izquierdo y un derecho, los cuales a su vez hacen referencia a "null", o mas dicho en prolog seria "nil", que significa vació.
En prolog un árbol binario se definirá de la siguiente manera
arbol(Hi,X,Hd), donde Hi es hijo izquierdo , Hd hijo derecho, y X el padre.
una vez explicado breve mente les paso a compartir estos ejercicios, espero les sirva.
Implementacion:
- % Autor: Joel Fernandez Segura
- % Fecha: 13/05/2014
- concatenar([],L,L).
- concatenar([A|Ca],L2,[A|Cc]):- concatenar(Ca,L2,Cc).
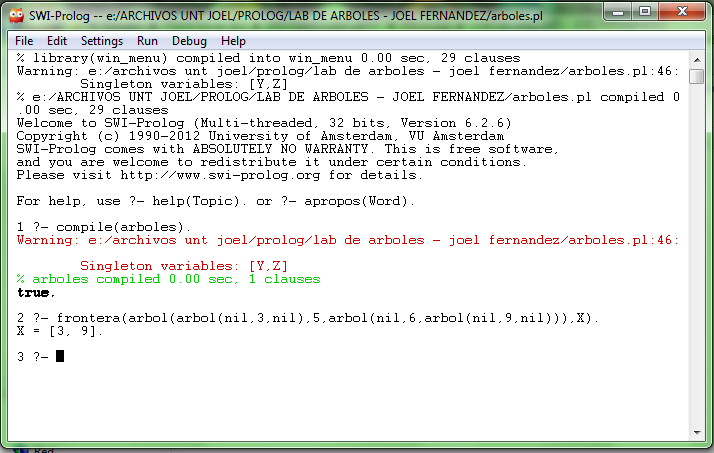
- %-------------------frondera(A,F) donde A es arbol y F es la frontera de A-------
- frontera(nil,[]).
- frontera(arbol(nil,X,nil),[X]):-!.
- frontera(arbol(I,_,D),Fa):- frontera(I,Fi), frontera(D,Fd),concatenar(Fi,Fd,Fa).
- %--------------------fronteras_iguales(A1,A2).-----------------------------------
- fronteras_iguales(A1,A2):- frontera(A1, F1),
- frontera(A2, F2),
- igual(F1, F2).
- pertenece(X,[X|_]):-!.
- pertenece(X,[_|Y]):-pertenece(X,Y).
- igual([],_).
- igual([L1|Lc],L2):- pertenece(L1,L2),igual(Lc,L2).
- % ----------------------------in_orden(A1,A2)------------------------------------
- in_orden(nil,[]).
- in_orden(arbol(I,X,D),A2):- in_orden(I,L1),in_orden(D,L2),
- concatenar(L1,[X],L3),
- concatenar(L3,L2,A2).
- % --------------------------pre_orden(A1,A2)------------------------------------
- pre_orden(nil,[]).
- pre_orden(arbol(I,X,D),A2):- pre_orden(I,L1),pre_orden(D,L2),
- concatenar([X],L1,L3),
- concatenar(L3,L2,A2).
- %---------------------------pos_orden(A1,A2)-------------------------------------
- pos_orden(nil,[]).
- pos_orden(arbol(I,X,D),A2):- pos_orden(I,L1),pos_orden(D,L2),
- concatenar(L1,L2,L3),
- concatenar(L3,[X],A2).







SOCIALIZA ESTO →